Introduction
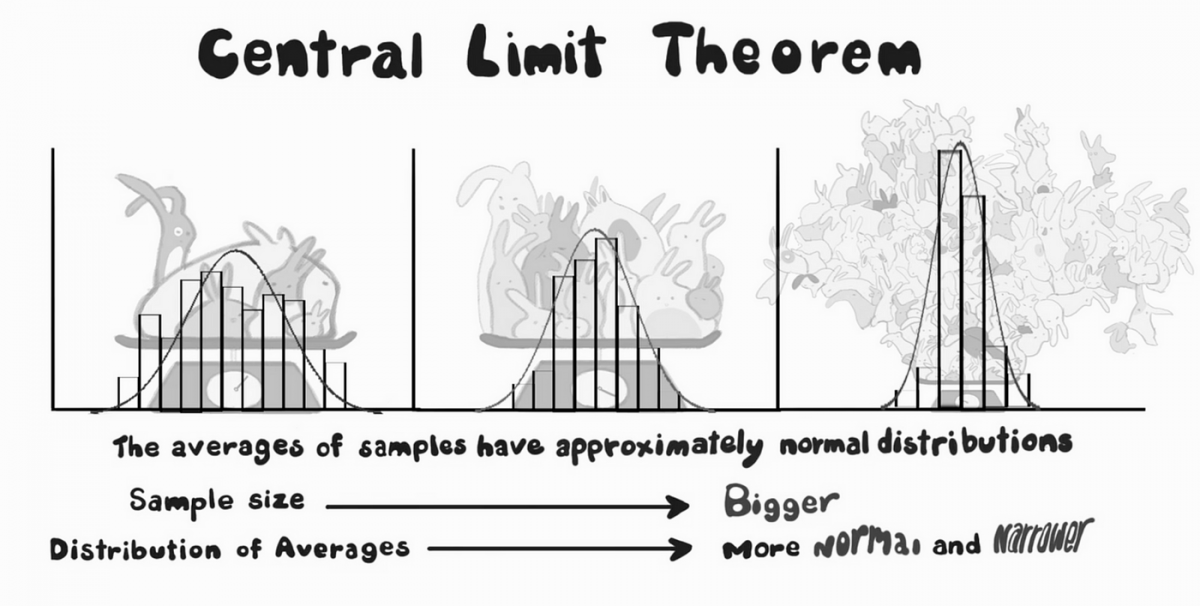
The Central Limit Theorem (CLT) is a fundamental concept in statistics that holds great relevance in decision-making processes. It states that when independent random variables are added, their sum tends to follow a normal distribution, regardless of the shape of the original variables’ distribution. This mental model is anchored in human psychology as we strive to make sense of complex data and draw meaningful conclusions. Understanding the CLT and its prevalence in our day-to-day lives is essential for making informed decisions based on accurate statistical reasoning.
Defining the Central Limit Theorem
The Central Limit Theorem is a statistical principle that describes the behavior of the sum or average of a large number of independent random variables. It states that as the sample size increases, the distribution of the sample mean tends to approximate a normal distribution, regardless of the underlying distribution of the individual variables. This theorem enables statisticians and decision-makers to make more accurate predictions and draw valid inferences from data.
Relevance of the Central Limit Theorem in Decision-Making
The CLT holds immense relevance in decision-making processes, especially when dealing with large datasets or multiple observations. It provides a powerful tool for understanding the behavior of sample means and the likelihood of specific outcomes. By leveraging the CLT, decision-makers can make more robust and reliable conclusions based on statistical analysis, leading to better-informed choices.
Examples of the Central Limit Theorem in Different Contexts
- Personal Life Decisions: Suppose an individual is considering investing in the stock market. By applying the CLT, they can analyze the historical returns of a diversified portfolio and estimate the mean return and the associated level of risk. Failing to understand the CLT, they may focus on individual stock performance without considering the broader portfolio’s behavior, leading to irrational investment decisions.
- Business Scenarios: In the manufacturing industry, quality control is critical. By utilizing the CLT, businesses can perform statistical sampling to monitor product quality. For instance, a company might measure the average weight of a sample of products to ensure it falls within acceptable limits. Failing to grasp the CLT, they may rely on limited sample sizes or improper sampling methods, leading to incorrect quality assessments and potential product defects.
- Public Policy-Making: The CLT plays a role in public policy-making when estimating population parameters based on sample data. For example, when conducting surveys to gauge public opinion on policy issues, the CLT enables policymakers to draw valid conclusions from a representative sample. Neglecting the CLT, policymakers may base decisions on small or biased samples, resulting in policies that do not reflect the true sentiments of the population.
Mental Biases and Psychological Underpinnings of the Central Limit Theorem
Several mental biases and psychological factors can contribute to misinterpretations of the CLT
- Confirmation Bias: Confirmation bias can lead individuals to seek or interpret information in a way that confirms their pre-existing beliefs or expectations. When dealing with the CLT, this bias can prevent individuals from adequately considering and analyzing data that may challenge their initial assumptions.
- Representativeness Heuristic: The representativeness heuristic can influence decision-making by relying on mental shortcuts and stereotypes. When applying the CLT, individuals may make assumptions based on their perceptions of what a “typical” distribution should look like, potentially leading to incorrect conclusions.
- Anchoring Bias: Anchoring bias occurs when individuals rely too heavily on initial information or reference points when making judgments or estimates. When using the CLT, individuals may anchor their interpretations to specific initial data, overlooking the broader implications of sample sizes and the tendency of means to approximate normal distributions.
Strategies to Identify and Avoid the Central Limit Theorem Trap
To avoid the pitfalls associated with misinterpreting the CLT, consider the following strategies
- Understand Sample Size: Recognize the significance of sample size in statistical inference. Larger sample sizes tend to yield more accurate and reliable results, aligning with the CLT. Be cautious when drawing conclusions based on small sample sizes, as they may not accurately represent the underlying population.
- Perform Sensitivity Analysis: Conduct sensitivity analyses to explore the impact of different assumptions and sample sizes on the outcomes. By examining how variations in inputs affect the results, decision-makers can gain a better understanding of the robustness of their conclusions.
- Seek Statistical Expertise: When dealing with complex statistical concepts such as the CLT, consider consulting statisticians or experts who can provide guidance and ensure accurate interpretation of data. Their expertise can enhance decision-making processes and mitigate potential biases.
- Update Assumptions and Conclusions: Stay open to updating assumptions and conclusions based on new data or insights. Recognize that the CLT is a powerful tool, but its assumptions may not always hold in every situation. Continuously assess the validity of your interpretations and adjust them as necessary.
Conclusion
The Central Limit Theorem serves as a cornerstone in statistical analysis and decision-making. Understanding its implications and potential pitfalls is crucial for making informed choices based on accurate data interpretation. By recognizing the psychological biases that can distort our understanding of the CLT and employing strategies such as considering sample sizes, performing sensitivity analyses, seeking expert advice, and remaining open to updating conclusions, individuals can navigate decision-making processes with more confidence and statistical rigor. Being aware of the Central Limit Theorem’s implications and actively avoiding cognitive biases associated with it empowers us to make better-informed decisions that align with our best interests.